Wind Farm Model for Power System Stability
Ph. D. student Hector A. Pulgar-Painemal with adviser P. Sauer
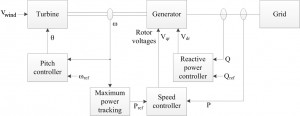
Wind farms based on Type-C wind turbine generators (WTGs) were modeled. Based on time scale decomposition, two detailed dynamic models were considered. Both models included a rotor speed controller, a reactive power controller and a pitch angle controller. The turbine aerodynamic was represented by a static model and a single-mass model was assumed. With respect to the controllers, the speed controller was designed to extract maximum power from the wind for a given wind speed. The reactive power controller was designed to follow a reference. The pitch angle controller was designed to limit the maximum active power output. All controllers used proportional and integral control. The control scheme is shown in Figure 16. Modal and bifurcation analysis was performed revealing that the WTG’s variables did not exhibit major oscillatory behavior when the system was perturbed. Moreover, the WTG’s variables did not participate in unstable modes and they did not change the system stability structure. In general, the most important interaction between WTGs and the system was the power interchange. This suggested that a model order reduction based on a positive power injection or a negative load was possible. In the case of a wind farm, the turbines were represented by an equivalent WTG and an equivalent wind (aggregated model). Aggregation techniques were used.
The aggregated model order was reduced by using selective modal analysis. This technique focuses on the most relevant modes and variables. Irrelevant variables were expressed in terms of the relevant ones, which reduced the model order. Replacing either a two-axis or zero-axis model of a WTG for the reduced-order model neither considerably altered the original system dynamics nor modified the system variables. An important reduction of simulation time and model complexity was obtained. In the largest case, it was shown that two wind farms that together are represented by 500 differential equations and 800 algebraic equations could be represented by just 4 differential equations.
This research is supported by a Fulbright Fellowship and the Grainger Center for Electric machinery and Electromechanics.