Developing a Time-Resolution Based Hierarchy of Models for Distributed Energy Resources
Post-doc Olaoluwapo Ajala with advisor A. Domínguez-García
As adoption of distributed energy resources (DERs) has accelerated, so has the need for comprehensive mathematical tools to model such systems. These models are utilized to analyze and control tasks necessary to develop innovative control and coordination technologies. For example, to design and test frequency controllers, models are needed to capture phenomena in the same time scale as the frequency, while neglecting phenomena in faster time scales. Although accurate mathematical models can be developed for DERs by utilizing concepts from circuit-theoretic and control theory, these are often highly complex and too detailed for the application. By simplifying them to show less detail, they can represent the phenomena relevant to the application of interest.
Figure 2. RegD signal response of an inverter-interfaced battery storage system
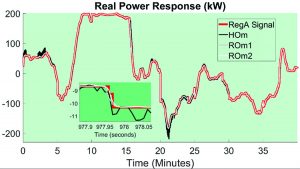
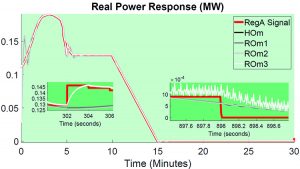
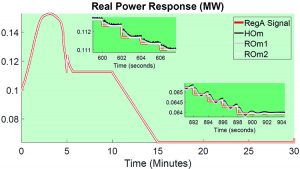
Our main contribution is the development of a time-resolution based hierarchy of models for DERs. Using Kirchhoff’s laws, component terminal relations, and relevant control laws, a high-order model is created. Afterward, reduced-order models are formulated from the high-order model using singular perturbation techniques for model-order reduction. The time resolution for which the reduced-order models is valid is also identified, and all models are explicitly presented with the parameters used for singular perturbation analysis identified.
Figure 3. RegA signal response of a micro-turbine system
Figures 2–4 depict a comparison of the reduced-order models we developed in this work with high-order models commonly used in the field. This research is supported by DOE.
Figure 4. RegA signal response of wind-turbine generator system