Grainger CEME

Ali Davoudi with adviser P.L. Chapman

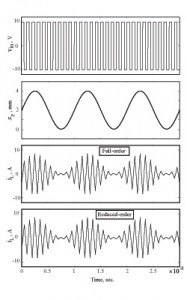
Figure 25 Input voltage, moving leg position, and input current resulted from full- and reduced-order HFMEC model of a plunger.

Electromechanical systems are faced with many compromises in simulation speed, accuracy, and stability. Magnetic-domain components ought to be accurate over a wide dynamic range, but they are often represented by analytical models that suffer from unreliable gross approximations. Alternatively, physics-based high-order models are obtained from finite-element method (FEM) or high-fidelity magnetic equivalent circuits (HFMEC). However, these high-order models are computationally intensive and incorporating relative motion is not a trivial task.

A detailed HFMEC model is developed that avoids commonly made geometrical simplifications. High-frequency eddy-current losses are represented with a long R-L ladder structure in the magnetic domain, modularly developed from position-dependent flux tubes. Moreover, the relative movement in FEM is facilitated by discretizing the movement path. For each discreet point on the movement path, the formulated FEM preserves the state matrix dimension. However, full-order models introduce thousands of state variables and are computationally intensive.

Model order reduction techniques break these compromises and provide analysts with accurate, physics-based models that have low order and fast execution time. Automated linear order-reduction techniques are considered to mathematically extract the essential dynamics in the desired bandwidth, thus preserving both accuracy and computational efficiency. Piecewise linear order-reduction methods are adopted to incorporate nonlinearities caused by relative motion and saturation. Figure 25 shows the applied PWM input voltage, sinusoidal mechanical position, and resulted full- and reduced-order current waveforms in a plunger. Computational efficiency is greatly improved as the system order is reduced from the original 300 to only 3, while preserving accuracy.