A 3-D Finite Element Analysis of Large-Scale Nonlinear Dynamic Electromagnetic Problems by Harmonic Balancing and Domain Decomposition
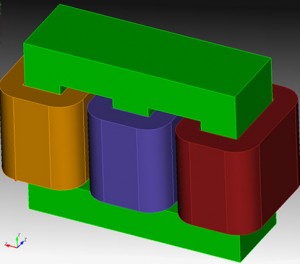
Figure 6: Simulation of three-phase inductor
Wang Yao with advisers J. M. Jin and P. T. Krein
The dual-primal finite element tearing and interconnecting (FETI-DP) method is applied together with the harmonic balance (HB) method and the fixed-point (FP) method to improve the efficiency of three-dimensional finite element analysis (FEA) of large-scale nonlinear dynamic electromagnetic problems. The FETI-DP method decomposes the original problem into smaller sub-domains problems. Combined with parallel computing techniques, the total computation time can be reduced significantly. To account for nonlinear B-H characteristics, the FP method is applied together with the polarization formulation. Since the FP method assumes a constant reluctivity, it decouples the systems of different harmonics. The FETI-DP method can then be applied to speed up the simulation of each harmonic in each FP iteration. Two benchmark problems and a three-phase inductor are simulated by the proposed method to validate the formulation and demonstrate its performance.
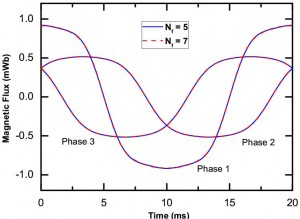
To validate our algorithm and demonstrate its performance, we simulate a three-phase inductor, shown in Fig. 6. This problem consists of an iron core and three windings, which are wound on the three limbs of the core. The three windings carry three-phase ac currents with MMF equal to 50 A-turns. We extract the magnetic fluxes in the center limb when three phases are excited independently. The simulation results with up to the fifth and seventh harmonics are plotted in Fig. 7. As can be seen, the magnetic iron core has been driven to saturation in all three cases. It is observed that the HB simulation converges when up to the seventh harmonic is included. For this simulation, the whole computational domain is meshed into 226,125 tetrahedral elements. In order to obtain better accuracy, second-order basis functions are used. This produces a total of 1,125,474 DOFs. METIS is used to partition the computational domain into 128 subdomains, which leads to approximately ten thousand DOFs inside each subdomain. The total computation time with 128 processors is 799 seconds. For comparison, the traditional FEA took 11.73 hours to solve this problem using four processors on the same computer.
This research is supported by the Grainger Center for Electric Machinery and Electromechanics.