Quantifying Uncertainties in Electric Machine Design
CEME Collaborators Dionysios Aliprantis (ECE) and Ilias Bilionis (ME) – Purdue University
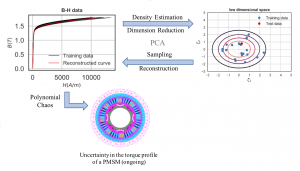
The uncertainty in the magnetic properties of steel, as exhibited by the B-H curve, is induced by variations in the manufacturing process and/or the supply chain. This uncertainty affects the rotor and stator of permanent magnet synchronous machines (PMSM) and consequently the output torque. Since last spring, we have developed a new method of quantifying the uncertainty in the B-H curve, which relies on a set of experimental measurements. Our approach, depicted in Fig. 1, starts by carrying out principal component analysis (PCA) on the available B-H dataset. Then, it projects the original data to a low-dimensional linear space and performs density estimation in that space. Finally, one can obtain samples of the B-H curve by sampling in the low-dimensional space, and reconstructing the corresponding B-H curve by following the inverse of the PCA projection. Furthermore, the low-dimensionality of this characterization makes the problem of propagating uncertainties amenable to response surface methodologies. Currently, we are at the stage of building a finite element solver for PMSM. After verifying and validating the code, we will proceed to the uncertainty propagation step. We will quantify the effect of B-H curve uncertainty on the torque profile, e.g., the torque ripple. Our technical approach will depend on the construction of an inexpensive polynomial chaos surrogate of the B-H curve-to-torque-ripple response surface. This research is supported by the Grainger Center for Electric Machinery and Electromechanics.