Power-Flow Modeling for Inverter-based Systems
PhD student Temitope Amuda with advisor A. Domínguez-García
Commercial power-flow solvers compute the solution to single slack-based power-flow problem using conventional approaches such as the Newton-Raphson or Gauss-Seidel method. In the conventional power-flow formulation, a single bus with a fixed normalized voltage and angle is dedicated to carry all the slack in the network. Alternatively, a distributed slack-based power flow formulation which does not depend on a single bus to carry the slack in the network has gained importance in inverter-based power systems. In the distributed slack-based formulation, the generator buses in the network all share the slack according to their participation factors. Commercial solvers cannot directly be utilized to implement and solve the distributed formulation. To this end, we propose Quasi-Newton methods to implement and solve distributed the slack-based power-flow formulation on commercial solvers. The proposed Quasi-Newton methods make use of modified Jacobian matrices in order to simplify the formulation into sub-problems which can then be solved by the commercial solvers.
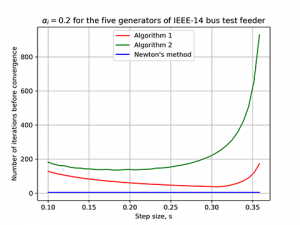
The results of two of the algorithms developed are shown in Figure 25 below. The convergence rate of two algorithms developed were compared to the classical Newton’s method on a modified IEEE 14-bus test feeder. The participation factor of the five generators was set as 0.2 each so that all the generators can share the slack in the network instead of dedicating a slack bus in the network. The algorithms converged to the true solution of the power-flow problem as desired when the step size is chosen within a certain boundary. This research is supported by the Department of Energy.