Mathematical Field Computation as an Analytical Tool for Electric Machines
Tim O’Connell with adviser PhilipT. Krein
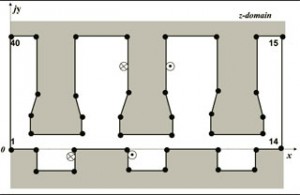
Figure 3 Forty-vertex air-gap polygon with two source coils representing a salient stator, slotted rotor machine.
The domain of achievable electric machine topologies is growing quickly, given the recent increase in the availability of inverters, exotic permanent magnet materials, and low-cost, precision manufacturing. These new possibilities require the advancement of available design tools. While finite element analysis (FEA) is a powerful analysis tool that is fairly easy to use and widely available in a number of commercial software packages, its utility in design is less obvious. Using FEA, it is often difficult to see the relationships between various input and output parameters with14 out extensive and time-consuming iterations. Frequently, the necessary accuracy needed for a given problem cannot be achieved without unreasonable computer run times.
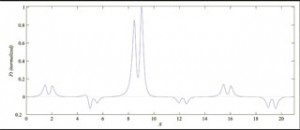
Figure 4 Normalized tangential force density distribution in the forty-vertex motor cross section along the center of the air gap.
An alternative method to FEA for electric machine design and analysis applies Schwarz- Christoffel (SC) conformal mapping theory using the SC Toolbox for MATLAB®. In this method, a two-dimensional (2D) developed machine cross-section domain is mapped via SC transformation to a concentric cylinder domain where solutions for the electromagnetic (EM) fields are known. These solutions are mapped back to the original domain, thus solving the original problem. All mapping is done via the SC Toolbox. With a locally accurate field solution now available, path-independent Maxwell stress tensor (MST) theory can successfully be implemented to calculate the rotor forces. This is a more accurate method than alternatives typically used when working with FEA field solutions.
This procedure has been successfully implemented to calculate the EM field in the air gap of and the force on the rotor of various 2D developed machine cross-sections. The numerical accuracy of the results has been verified by comparing the solutions with magnetic-equivalent circuit-derived coenergy solutions as the air gap gets small. As one example, consider the 40-vertex air-gap polygon in Figure 3 representing a machine with a salient pole stator and slotted rotor. One-turn, 1-A coils are placed on both the stator and rotor as shown. Intuitively, we expect the rotor to be pulled to the right, and the results verify this. The tangential force density profile along the center of the air gap is shown in Figure 4. Clearly, integrating this waveform to calculate the total rotor tangential force will give a positive value, indicating a rightward force. We note that the force density is concentrated in sharp peaks at the corners of the stator and rotor teeth. An FEA calculation would need a dense mesh in these regions in order to achieve a reasonable accuracy, whereas the SC formulation automatically handles sharp corners with ease. Initial results with the SC mapping method have been successful and its potential seems encouraging, but many implementation details still remain to be worked out before considering this as a viable design alternative to FEA.