Low-Order Nonlinear Dynamic Models Extracted from a Finite Eelement Method–Based State-Space Formulation for Magnetic Devices
Liyan Qu with adviser Patrick L. Chapman
Finite-element (FE) based models for magnetic devices can be set up automatically, given the geometrical data and material information. However, time-domain, FE-based modeling is computationally expensive. This project deals with nonlinear model order reduction (MOR) methods for extracting low-order dynamic models of nonlinear magnetic devices from a high-order physics-based FE model. These methods are based on a piecewise linear approach with Krylov subspace projection. They enable physics-based models to be implemented without heuristic assumptions or excessive computation and are demonstrated with an example inductor model and verified experimentally. Simulation results show that the original, nonlinear high-order system is well represented by a piecewise set of connected low-order, linear systems. Synthesis of these methods can be fully automated so the end user can rapidly model new devices without repeating sophisticated mathematics. This project provides a foundation for modeling more complicated magnetic devices, such as multiphase coupled inductors, actuators, and rotary machines.
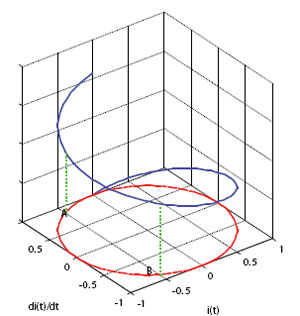
Current work is focused on developing low-order 2D FE analysis (FEA) models with hysteresis and multiple windings. Selection of the reduced models needs to be done in a 2D or 3D space. A periodic output current with a constant magnitude corresponds to one loop in the plane of i(t)-di(t)/dt, the current and its derivative (shown in Figure 19). Many loops of this kind can be set up. Then, to distinguish them, another dimension (z-axis shown in Figure 19) is added to represent the magnitude of the currents. (When there are points with the same value and derivative such as A and A’ but corresponding to a different magnitude, the z axis is necessary.) FE–based numerical modeling of electrical machines and power transformers always involves a multiple-winding magnetics model. The wire-by-wire model presented can be extended to an arbitrary number of windings (or solid conductors) by introducing corresponding circuit equations, which must be coupled with field equations and solved simultaneously. The current problem for multiple windings is to find an efficient method to set up and select reduced models.