Gauss-Seidel Power-Flow Convergence with Negative Reactance Values
Rodney Yeu with his adviser Peter Sauer
The conventional method of modeling two-winding tap-changing transformers and three-winding transformers may lead to negative leakage reactance values. This may cause instability of transient simulations as well as divergence of the steady-state power flow analysis. Specifically, negative reactance has been shown to cause divergence of the Gauss-Seidel power-flow analysis while the same system analyzed using the Newton- Raphson method converges.
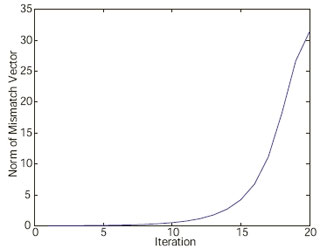
It was observed that negative reactance causes the region of convergence to be very small or even nonexistent. This is seen by looking at the mismatch vector as the iteration reaches the power-flow solution. For example, Figure 26 shows the divergence of the Gauss-Seidel power flow sequence when the initial estimation was made close enough to the actual solution so that the initial norm of the mismatch vector was 0.035. The negative reactance can cause divergence of the Gauss-Seidel power flow even with the initial estimation close to the actual solution.
Traditionally there have been two ways to avoid the divergence of the Gauss-Seidel power flow caused by negative reactance. One is to use a simplified model of the transformer to get rid of the negative reactance value. Another is to omit the Gauss-Seidel method and use another method such as the Newton- Raphson method. These methods circumvent the divergence problem and mitigate the possible advantages of the Gauss-Seidel method. Since the region of convergence using Newton’s method differs from that of the Gauss-Seidel method, it is possible that power systems not solvable by Newton’s method may be solved by the Gauss-Seidel method. Therefore, the divergence of the Gauss-Seidel power flow and possible methods to make it converge will be investigated.