Grainger CEME

Wang Yao with advisers J. M. Jin and P. T. Krein

Figure 9: The IEEJ model.

Efficiently delivering and utilizing energy are among the most challenging topics for power engineers. As one of the largest fossil energy consumers, electric machines have to be designed to operate at a high power density, optimal efficiency, and high degree of reliability. All these requirements necessitate accurate performance prediction at the design stage. In this research, we adopted the finite element method, one of the most powerful numerical schemes, to analyze electric machine problems. We implemented higher-order vector finite elements with curvilinear edges to accurately model the complex geometry of electric machine problems and fast-varying magnetic fields. To reduce computation time, we adopted the A-V formulation, which has both magnetic vector and the electric scalar potentials, with the generalized minimal residual method and the incomplete LU preconditioner. Several linear benchmark problems, including both megnetostatic and eddy current problems were tested. Next, we implemented the Newton-Raphson method to deal with nonlinear problems. Cubic splines and the relaxation factor were utilized to ensure global convergence.

Figure 10: The magnetic flux density distribution in the IEEJ model.

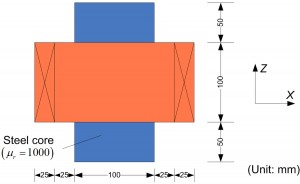
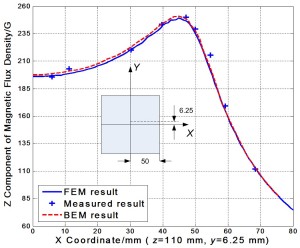
We tested several benchmark problems to validate our numerical scheme. One, proposed by the Institute of Electrical Engineers of Japan, is presented here. The problem contains a rectangular iron core surrounded by a racetrack coil. The iron core has a high relative permeability of 1000. A side view is illustrated in Figure 9. The magnetic flux density along a line is extracted and compared with measurement results and the boundary element method results in Figure 10. We found a good agreement between these results.

This research is supported by the Grainger Center for Electric Machinery and Electromechanics.