Grainger CEME

Sairaj Dhople with advisor Alejandro Domínguez-García

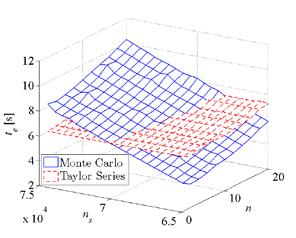
Figure 42: Execution time to compute the pdf of a performability metric using the proposed method and through Monte Carlo simulations.

A common concern with Markov reliability and reward models is that model parameters, i.e., component failure and repair rates, are seldom perfectly known. This work proposes a numerical method based on the Taylor series expansion of the underlying Markov chain stationary distribution to propagate parametric uncertainty to reliability and performability indices of interest. The Taylor series coefficients are expressed in closed form as functions of the Markov chain generator-matrix group inverse. Given distributions of the model parameters,
random variable transformations are applied to compute the probability distributions of the reliability and performability indices. A significant advantage of the proposed framework is that only the parametrized Markov
chain generator matrix is required as an input, i.e., closed-form expressions for the reliability and performability indices as a function of the model parameters are not needed. Analysis of large models demonstrates lower
execution times compared to Monte Carlo simulations. For instance, Figure 42 depicts the execution time, te, to compute the distribution of a performbaility metric as a function of the number of random samples used in the Monte Carlo simulation, ns, and the model order, n. As seen in the figure, as n increases, the proposed method outperforms Monte Carlo simulations in terms of execution time. The effect is more pronounced as the number of samples in the Monte Carlo simulation is increased.

This work was supported in part by the National Science Foundation under grant ECCS-CAR-0954420.