Grainger CEME

Wang Yao with Advisors J.M. Jin and P.T. Krein

Figure 6: Comparison of the magnetic flux ensity of TEAM problem 21a-2

The dual-primal finite element tearing and interconnecting (FETI-DP) method is adopted together with the tree-cotree splitting (TCS) method to shorten the computation time of 3-D eddy current problems. The FETI-DP method, among various domain decomposition methods, can provide a balanced load distribution over processors. Therefore, it can fully decouple the original large problem and exhibits an excellent numerical scalability. The
FETI-DP algorithm has been successfully adopted in computational mechanics, acoustics and electromagnetics. It has not been applied in the electric machine area largely due to the low-frequency breakdown problem. Most electric machine problems can be categorized into quasi-static problems. But the finite-element method (FEM) with vector basis functions may break down at low frequencies due to illconditioned system matrices. The TCS method is applied to overcome this obstacle. The general principle of the TCS algorithm is first to construct a minimum spanning tree over the finite-element mesh. Next, the degrees of freedom associated with the tree edges are eliminated to regularize the ill-conditioned system matrix.

Figure 7: Speedup with respect to the number of processors

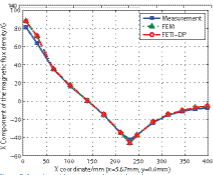
We solve the benchmark TEAM problem 21a-2 to validate our algorithm and demonstrate its capability. The problem consists of two identical racetrack coils with currents in opposite directions and one conducting plate with two slots. The whole computational domain is decomposed into 128 subdomains. The total number of FEM unknowns, interface unknowns, and corner unknowns are 1.1 × 106, 8.7 × 104, and 6.2 × 102, respectively. The BiCGSTAB method is used to solve the interface problem and convergence tolerance is set to be 1 × 10-4. In Figure 6 we compare the results using the FETI-DP scheme with measured results and those computed from standard FEM (without domain decomposition).
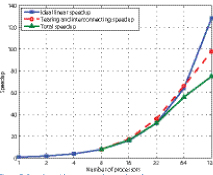
As can be seen, the FETI-DP results agree well with both measured and FEM results. To investigate the parallel efficiency of our scheme, we record the total wall-clock time and the time for tearing and interconnecting, including LU factorization, solving the interface problem, and recovering. We define speedup with respect to the wall-clock time of eight processors. As can be seen from Figure 7, a reasonable speedup can be achieved for this case of up to 128 number of processors.

This research was supported by the Grainger Center for Electric Machinery and Electromechanics.